1.8. JAK OCENIĆ „NORMALNOŚĆ” ROZKŁADU

W analizie statystycznej często zakłada się, że dane pochodzą z rozkładu normalnego, co ułatwia wiele obliczeń i testów. Jednak zanim przystąpimy do analizy danych, ważne jest ocenienie, czy dane rzeczywiście pochodzą z rozkładu normalnego. W dzisiejszym wpisie omówimy metody oceny „normalności” rozkładu danych.

Histogramy i Wykresy Q-Q:

1. Histogram to wykres, który przedstawia rozkład danych w postaci słupków. Jeśli rozkład jest zbliżony do rozkładu normalnego, histogram będzie przypominał dzwon (tzw. rozkład dzwonowy).

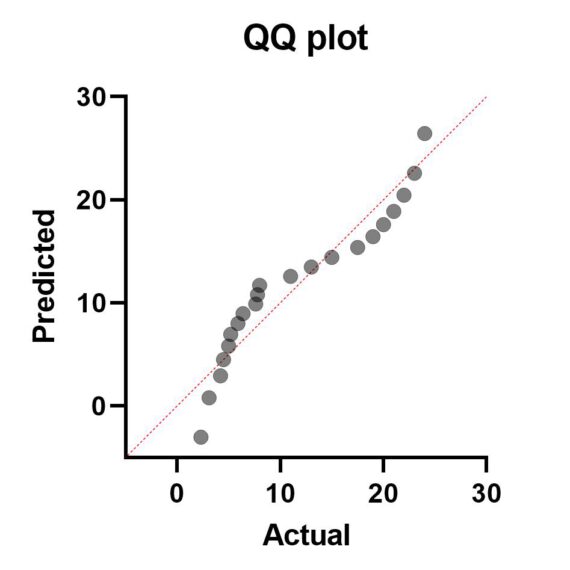
2. Wykresy Q-Q (Quantile-Quantile) to narzędzie pozwalające porównać dane z rozkładem normalnym. Na wykresie Q-Q rzeczywiste dane są przedstawione na osi X, a teoretyczne kwantyle rozkładu normalnego na osi Y. Jeśli punkty na wykresie Q-Q zbliżają się do prostej linii, oznacza to, że dane są zbliżone do rozkładu normalnego.

Testy Statystyczne:

1. Test Shapiro-Wilka: Jest to jeden z najpopularniejszych testów normalności. Test ten oblicza statystykę testową opartą na różnicy między wartościami obserwowanymi, a wartościami oczekiwanymi w rozkładzie normalnym. Jeśli p-wartość wynosi mniej niż ustalony poziom istotności (na ogół 0,05), to odrzucamy hipotezę o normalności (uznajemy, że dane nie mają rozkładu normalnego). O tym, jak to działa w praktyce, opisaliśmy w artykule „Rozkłady prawdopodobieństwa: Klucz do zrozumienia statystyki”.

2. Test Andersona-Darlinga: To kolejny test oceny normalności, który jest mniej wrażliwy na duże próbki. Tak jak w przypadku testu Shapiro-Wilka, odrzucenie hipotezy o normalności zależy od p-wartości.

Statystyki opisowe:

Skośność i kurtoza to statystyki, które charakteryzują kształt i asymetrię rozkładu danych. Dla rozkładu normalnego, wartości skośności i kurtozy wynoszą odpowiednio 0 i 3. Zmiany od tych wartości mogą wskazywać na niestandardowy rozkład (inny niż rozkład normalny). Zapraszamy do lektury naszego wpisu „Statystyki opisowe dla zmiennych ilościowych”, gdzie omawiamy ten temat bardziej szczegółowo.

Warto pamiętać, że testy normalności nie są idealne, zwłaszcza w przypadku małych próbek. W praktyce ważne jest uwzględnienie kontekstu badawczego i nie poleganie wyłącznie na wynikach testów. Czasami nawet, jeśli dane nie spełniają założenia o normalności, można nadal stosować metody oparte na rozkładzie normalnym, jeśli inne założenia są spełnione i próbka jest wystarczająco duża. Jednak ocena „normalności” rozkładu danych jest istotnym krokiem w analizie statystycznej, który może wpłynąć na wiarygodność i trafność wyników.