1.7. ROZKŁADY PRAWDOPODOBIEŃSTWA: KLUCZ DO ZROZUMIENIA STATYSTYKI
Rozkłady prawdopodobieństwa to zagadnienie, które może wydawać się skomplikowane, ale postaramy się wyjaśnić je w sposób, który będzie zrozumiały nawet dla tych, którzy nie mają doświadczenia w tej dziedzinie.
Czym są rozkłady prawdopodobieństwa?
Rozkłady prawdopodobieństwa to matematyczne modele, które opisują, jakie są szanse na wystąpienie różnych zdarzeń. To narzędzie, które pomaga nam przewidywać, jakie wyniki możemy oczekiwać w różnych sytuacjach. W statystyce rozkłady prawdopodobieństwa są niezwykle ważne, ponieważ pozwalają nam analizować dane i podejmować decyzje na podstawie prawdopodobieństwa. Więcej na ten temat przeczytasz w naszym artykule „Statystyka opisowa vs. Statystyka wnioskowa”.
Rozkład Normalny
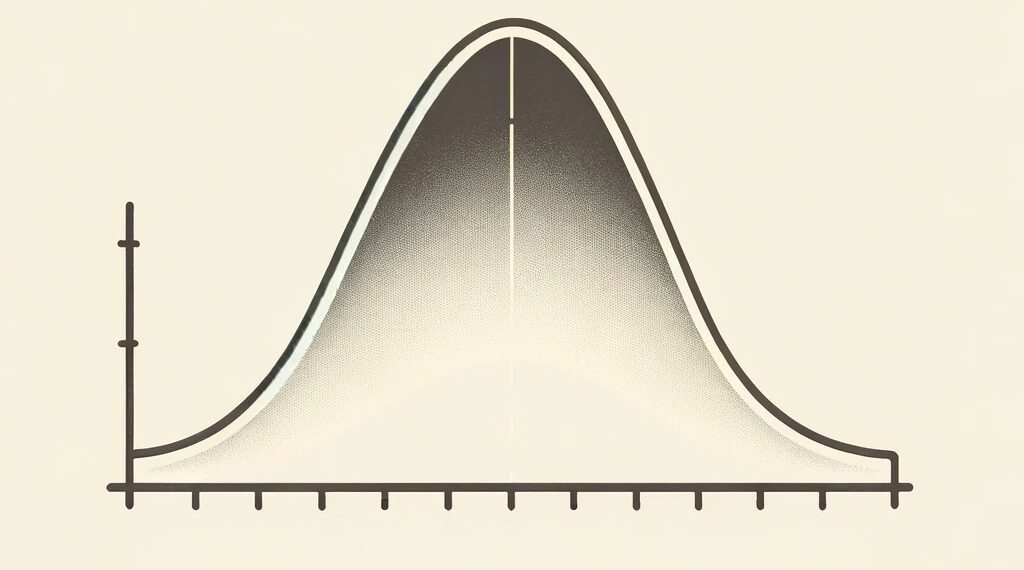
Jeden z najważniejszych rozkładów prawdopodobieństwa, z którym często mamy do czynienia, to rozkład normalny, nazywany także rozkładem Gaussa. Ten rozkład ma charakterystyczny kształt dzwonu i jest powszechnie spotykany w naturze.
Przykładowo, jeśli mierzymy wzrost ludzi w populacji, to rozkład normalny pozwala nam zrozumieć, że większość ludzi będzie mieć średni wzrost, a osoby znacznie wyższe lub niższe stanowią mniejszy odsetek populacji. Dzięki rozkładowi prawdopodobieństwa możemy obliczyć, jakie jest prawdopodobieństwo spotkania osoby o konkretnym wzroście w danej populacji. O tym, jak to działa w praktyce, opisaliśmy w artykule „Jak ocenić „normalność” rozkładu”.
Inne przykłady rozkładów prawdopodobieństwa
Oprócz rozkładu normalnego, istnieje wiele innych rozkładów prawdopodobieństwa, które są używane w statystyce w zależności od rodzaju danych i pytania badawczego. Oto kilka przykładów:
- Rozkład jednostajny – W tym rozkładzie wszystkie zdarzenia mają równe prawdopodobieństwo. Przykładem może być rzut monetą, gdzie wyrzucenie orła lub reszki ma takie same szanse.
- Rozkład Poissona – Ten rozkład jest używany, gdy chcemy modelować rzadkie zdarzenia, takie jak liczba telefonów alarmowych w danym czasie lub liczba wizyt na stronie internetowej w ciągu godziny.
- Rozkład wykładniczy – Rozkład ten jest używany do modelowania czasu między kolejnymi zdarzeniami, na przykład czasu między przyjściami klientów do sklepu.
Warto podkreślić, że rozkłady prawdopodobieństwa to fundamentalna część statystyki, która pozwala nam lepiej zrozumieć świat i podejmować bardziej racjonalne decyzje na podstawie danych. W kolejnych wpisach będziemy omawiać różne rodzaje rozkładów i jak stosować je w praktyce analizy statystycznej.
